一元线性回归

使用到的python库： 

1
2
3
4
5
6
7
import sys
import numpy as np
import matplotlib.pyplot as plt
from lab_utils_uni import plt_gradients
import copy
import math
from lab_utils_multi import  run_gradient_descent

问题陈述

一个1000平方英尺的房子以300,000美元售出，一个2000平方英尺的房子以500,000美元售出。请给出一个线性回归模型，呈现房子面积与售价的关系。

面积/1000平方英尺 价格/1000$
1 300
2 500

记录数据 

1
2
x_train = np.array([1.0,2.0])
y_train = np.array([300,500])

理论依据： 一元线性回归的预测函数为: 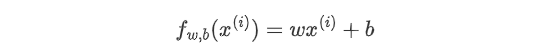误差函数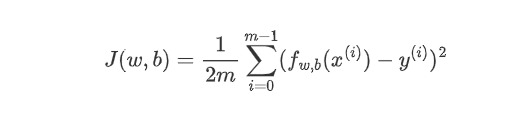： 梯度下降算法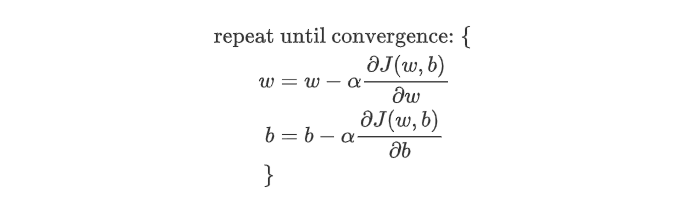： 其中，α为学习率，决定单次下降的幅度。

梯度为：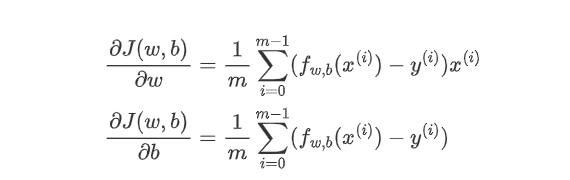

用代码实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#计算误差函数
def compute_cost(x,y,w,b):
    m = x.shape[0]#用m获取x数组的元素个数
    cost = 0
    for i in range(m):#从1到m累加误差
        f_wb = w*x[i]+b
        cost += (f_wb-y[i])**2
    total_cost = cost/(m*2)
    return total_cost

#计算偏导数的函数
def compute_gradient(x,y,w,b):
    m=x.shape[0]
    dj_dw=0
    dj_db=0
    for i in range(m):
        f_wb=w*x[i]+b
        #误差函数的单项分别对w和b求偏导
        dj_dw_i=(f_wb-y[i])*x[i]#变量命名中含有i，实现自动更新
        dj_db_i=(f_wb-y[i])
        #累加：
        dj_dw+=dj_dw_i
        dj_db+=dj_db_i
    #除以m，得到整个误差函数一次对w和b的偏导
    dj_dw=dj_dw/m
    dj_db=dj_db/m
    return dj_dw,dj_db

#计算梯度下降的函数
def gradient_descent(x,y,w_in,b_in,alpha,num_iters,cost_function,gradient_function):
    '''变量声明
      x (ndarray (m,))  : 解释变量
      y (ndarray (m,))  : 目标变量
      w_in,b_in (scalar): 参数w，b的初始值 
      alpha (float):     学习率
      num_iters (int):   梯度下降的次数
      cost_function:     计算误差的函数
      gradient_function: 计算偏导数的函数
      
    返回值：
      w (scalar)，b (scalar): 参数w，b的最终值，此时误差值达到局部最小
      J_history (List): 对每次梯度下降后的误差值做记录
      p_history (list): 对每次梯度下降后的参数w，b做记录
      '''
    #定义变量
    J_history = []
    p_history = []
    b = b_in
    w = w_in

    #通过循环拟合出使误差最小的w，b
    for i in range(num_iters):
        dj_dw,dj_db = gradient_function(x,y,w,b)#先计算出偏导数

        #梯度下降，同步更新w和b的值
        b = b-alpha*dj_db
        w = w-alpha*dj_dw

        #使用append添加记录每次循环得到的误差和参数w，b
        if i<100000:
            J_history.append(cost_function(x,y,w,b))
            p_history.append([w,b])
        
        #输出梯度下降过程的部分结果，看看规律，这部分并不是必要的
        if i%math.ceil(num_iters/10)==0:
            print(f"Iteration {i:4} Cost: {J_history[-1]:0.2e}",
                  f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e}",
                  f"w: {w: 0.3e}, b:{b: 0.5e}")

    return w, b, J_history, p_history #return w and J,w history for graphing

开始运行，示例： 

1
2
3
4
5
6
w_init = 1
b_init = 2
iterations = 10000
tmp_alpha = 1.0e-2
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha, iterations, compute_cost, compute_gradient)
print(f"(w,b) found by gradient descent: ({w_final:8.4f},{b_final:8.4f})")
输出结果： Iteration 0 Cost: 7.79e+04 dj_dw: -6.445e+02, dj_db: -3.965e+02 w: 7.445e+00, b: 5.96500e+00

Iteration 1000 Cost: 3.82e+00 dj_dw: -3.930e-01, dj_db:  6.358e-01 w:  1.946e+02, b: 1.08710e+02

Iteration 2000 Cost: 8.88e-01 dj_dw: -1.894e-01, dj_db:  3.065e-01 w:  1.974e+02, b: 1.04198e+02

Iteration 3000 Cost: 2.06e-01 dj_dw: -9.130e-02, dj_db:  1.477e-01 w:  1.987e+02, b: 1.02024e+02

Iteration 4000 Cost: 4.80e-02 dj_dw: -4.401e-02, dj_db:  7.121e-02 w:  1.994e+02, b: 1.00975e+02

Iteration 5000 Cost: 1.11e-02 dj_dw: -2.121e-02, dj_db:  3.433e-02 w:  1.997e+02, b: 1.00470e+02

Iteration 6000 Cost: 2.59e-03 dj_dw: -1.023e-02, dj_db:  1.655e-02 w:  1.999e+02, b: 1.00227e+02

Iteration 7000 Cost: 6.02e-04 dj_dw: -4.929e-03, dj_db:  7.976e-03 w:  1.999e+02, b: 1.00109e+02

Iteration 8000 Cost: 1.40e-04 dj_dw: -2.376e-03, dj_db:  3.844e-03 w:  2.000e+02, b: 1.00053e+02

Iteration 9000 Cost: 3.25e-05 dj_dw: -1.145e-03, dj_db:  1.853e-03 w:  2.000e+02, b: 1.00025e+02

(w,b) found by gradient descent: (199.9924,100.0122)

注意一下上面打印的梯度下降过程的一些特征。

  • 成本开始很大，并迅速下降，如讲座中的幻灯片所述。

  • 偏导数dj_dw和dj_db也会变小，一开始很快，然后越来越慢。如讲座中的图表所示，当过程接近 “碗底”时，由于该点上的导数值较小，所以进展较慢。

多元线性回归

使用到的python库： 

1
2
3
import copy,math
import numpy as np
import matplotlib.pyplot as plt

问题陈述

你将使用住房价格预测的例子。训练数据集包含三个例子，有四个特征（尺寸、卧室、楼层和，年龄），如下表所示。 请注意，与先前的实验室不同，尺寸的单位是平方英尺而不是1000平方英尺。这导致了一个问题，你将在下一个实验中解决这个问题。

尺寸（平方英尺） 卧室数量 楼层数量 房龄 价格（1000刀）
2104 5 1 45 460
1416 3 2 40 232
852 2 1 35 178

记录数据

1
2
x_train = np.array([[2104,5,1,45],[1416,3,2,40],[852,2,1,35]])
y_train = np.array([460,232,178])

参数向量w，参数b

1
2
b_init = 0
w_init = np.zeros(4,)

理论依据:

预测函数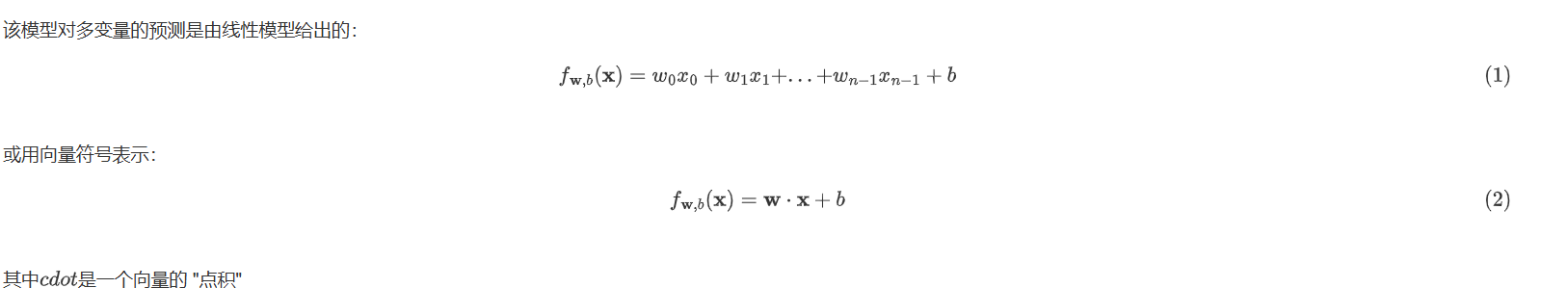

成本函数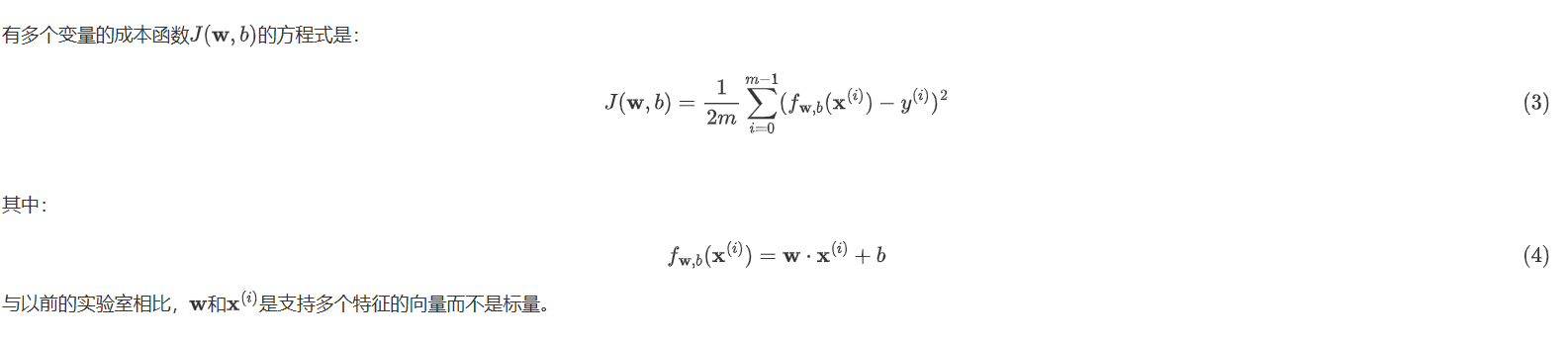

多变量梯度下降

代码实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
import copy,math
import numpy as np
import matplotlib.pyplot as plt

np.set_printoptions(precision=2)

#创建特征变量和目标变量
x_train = np.array([[2104,5,1,45],[1416,3,2,40],[852,2,1,35]])
y_train = np.array([460,232,178])

#计算误差：获取元素个数，初始化误差->累加误差的平方和->除以2m
def compute_cost(x,y,w,b):
    m = x.shape[0]
    total_cost = 0
    for i in range(m):
        f_wb_i = np.dot(x[i],w)+b
        total_cost+=(f_wb_i-y[i])**2
    cost = total_cost/(2*m)
    return cost

#计算梯度：获取元素个数，初始化偏导数->累加m个例子的误差，计算b的偏导->遍历w每个元素，计算偏导数->除以m
def compute_gradient(x,y,w,b):
    m,n = x.shape
    dj_dw = np.zeros(n,)
    dj_db = 0.
    for i in range(m):
        #计算误差
        err = np.dot(x[i],w)+b-y[i]

        #内循环用于逐个计算w中元素的偏导数
        for j in range(n):
            dj_dw[j] += err*x[i,j]
        
        #计算b的偏导数
        dj_db += err

    dj_dw = dj_dw / m
    dj_db = dj_db / m
    return dj_db,dj_dw

#多变量梯度下降：定义成本数组和参数w，b->逐次计算梯度，逐个梯度下降->返回
def gradient_descent(x, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters):
    # 一个数组，用于存储每次迭代的成本J和W，主要用于以后的绘图
    J_history = []
    w = copy.deepcopy(w_in)  #避免在函数中修改全局W
    b = b_in

    for i in range(num_iters):
        #先计算梯度
        dj_db,dj_dw = gradient_function(x,y,w,b)
        #同步更新
        w = w - alpha*dj_dw
        b = b - alpha*dj_db
        #保存误差
        if i <100000:
            J_history.append(cost_function(x,y,w,b))

        # 每隔10次就打印一次成本，如果<10，则打印相同次数的迭代
        if i% math.ceil(num_iters / 10) == 0:
            print(f"Iteration {i:4d}: Cost {J_history[-1]:8.2f}   ")
        
    return w, b, J_history #返回最终的w,b和J的历史记录，用于制图

#开始运行:
b_init = 0
w_init = np.zeros(4,)
num_iters = 1000
alpha = 5.0e-7
w_final,b_final,J_hist = gradient_descent(x_train,y_train,w_init,b_init,compute_cost,compute_gradient,alpha,num_iters)
print(f"最终找到的w为{w_final}，b为{b_final:0.2f}")
m = x_train.shape[0]
for i in range(m):
    print(f"预测值{np.dot(x_train[i],w_final)+b_final:0.2f}，实际值:{y_train[i]}\n")


# 绘制成本与迭代的关系图
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12, 4))
ax1.plot(J_hist)
ax2.plot(100 + np.arange(len(J_hist[100:])), J_hist[100:])
ax1.set_title("Cost vs. iteration");  ax2.set_title("Cost vs. iteration (tail)")
ax1.set_ylabel('Cost')             ;  ax2.set_ylabel('Cost') 
ax1.set_xlabel('iteration step')   ;  ax2.set_xlabel('iteration step') 
plt.show()

输出结果:

Iteration    0: Cost  2529.46   
Iteration  100: Cost   695.99   
Iteration  200: Cost   694.92   
Iteration  300: Cost   693.86   
Iteration  400: Cost   692.81   
Iteration  500: Cost   691.77   
Iteration  600: Cost   690.73   
Iteration  700: Cost   689.71   
Iteration  800: Cost   688.70   
Iteration  900: Cost   687.69   
最终找到的w为[ 0.2   0.   -0.01 -0.07]，b为-0.00
预测值426.19，实际值:460

预测值286.17，实际值:232

预测值171.47，实际值:178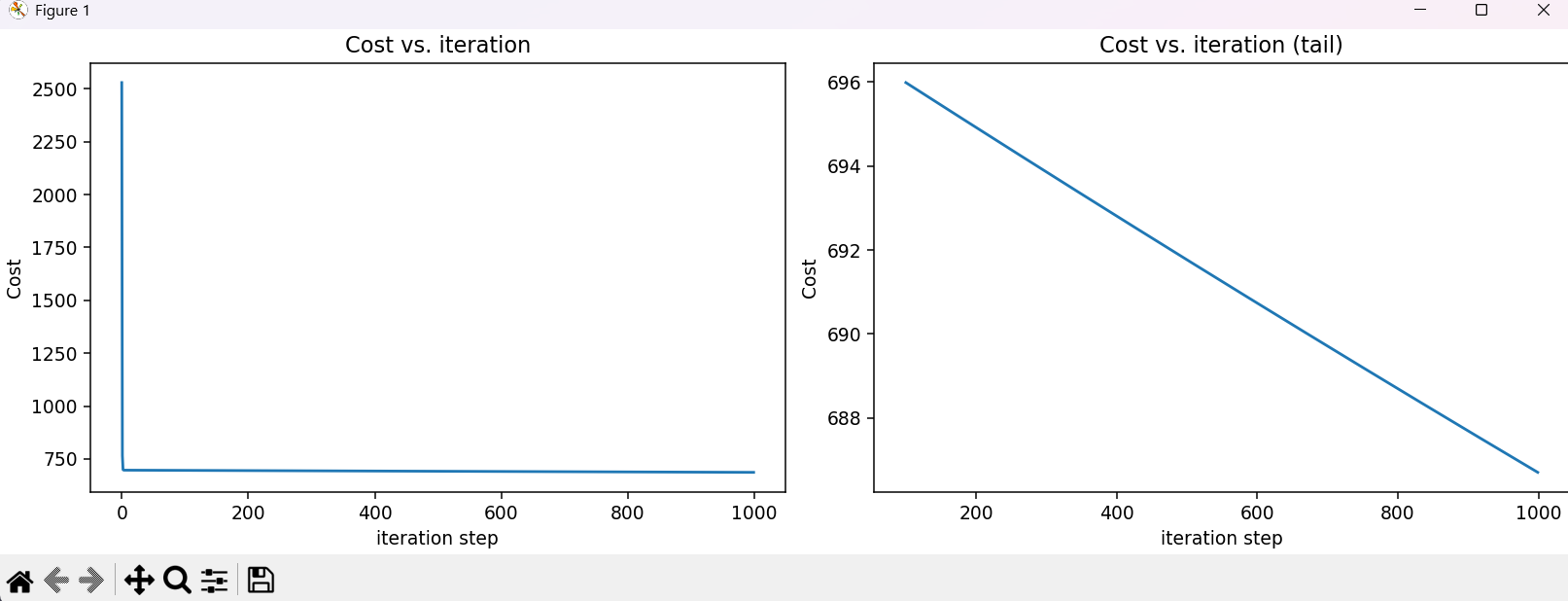

预测值和实际值地差别还是挺大的

解决办法：特征缩放

代码实现: 

1
2
3
4
5
def zscore_normalize_features(x):
    mu = np.mean(x,axis=0)
    sigma = np.std(x,axis = 0)
    x_norm = (x-mu)/sigma
    return x_norm,mu,sigma

现对x_train进行特征缩放，再进行梯度下降得到w，b 

1
2
3
x_norm,x_mu,x_sigma = zscore_normalize_features(x_train)
print(f"{x_norm}")
w_norm, b_norm, hist = run_gradient_descent(x_norm, y_train, 1000, 1.0e-1, )
输出结果：

Iteration Cost          w0       w1       w2       w3       b       djdw0    djdw1    djdw2    djdw3    djdb

---------------------|--------|--------|--------|--------|--------|--------|--------|--------|--------|--------|
        0 3.78405e+04  1.2e+01  1.2e+01 -4.1e+00  1.2e+01  2.9e+01 -1.2e+02 -1.2e+02  4.1e+01 -1.2e+02 -2.9e+02
      100 2.41945e-05  3.8e+01  4.2e+01 -3.1e+01  3.6e+01  2.9e+02  4.2e-05 -4.2e-05  6.3e-04  7.9e-05 -7.7e-03
      200 1.70488e-14  3.8e+01  4.2e+01 -3.1e+01  3.6e+01  2.9e+02  1.0e-09 -1.0e-09  1.5e-08  1.9e-09 -2.0e-07
      300 1.17254e-23  3.8e+01  4.2e+01 -3.1e+01  3.6e+01  2.9e+02  1.4e-14 -3.5e-14  3.7e-13  3.5e-14 -5.4e-12
      400 3.06962e-26  3.8e+01  4.2e+01 -3.1e+01  3.6e+01  2.9e+02  2.2e-14  2.0e-14  1.3e-14  2.3e-14 -2.5e-13
      500 3.06962e-26  3.8e+01  4.2e+01 -3.1e+01  3.6e+01  2.9e+02  2.2e-14  2.0e-14  1.3e-14  2.3e-14 -2.5e-13
      600 3.06962e-26  3.8e+01  4.2e+01 -3.1e+01  3.6e+01  2.9e+02  2.2e-14  2.0e-14  1.3e-14  2.3e-14 -2.5e-13
      700 3.06962e-26  3.8e+01  4.2e+01 -3.1e+01  3.6e+01  2.9e+02  2.2e-14  2.0e-14  1.3e-14  2.3e-14 -2.5e-13
      800 3.06962e-26  3.8e+01  4.2e+01 -3.1e+01  3.6e+01  2.9e+02  2.2e-14  2.0e-14  1.3e-14  2.3e-14 -2.5e-13
      900 3.06962e-26  3.8e+01  4.2e+01 -3.1e+01  3.6e+01  2.9e+02  2.2e-14  2.0e-14  1.3e-14  2.3e-14 -2.5e-13
w,b found by gradient descent: w: [ 38.05  41.54 -30.99  36.34], b: 290.00

现在来预测一个有1200平方英尺、3间卧室、1层楼、40年房龄的房子的价格。必须用训练数据归一化时得出的平均值和标准差对数据进行归一化。 

1
2
3
4
x_house = np.array([1200, 3, 1, 40])
x_house_norm = (x_house - x_mu) / x_sigma
x_house_predict = np.dot(x_house_norm, w_norm) + b_norm
print(f" predicted price of a house with 1200 sqft, 3 bedrooms, 1 floor, 40 years old = ${x_house_predict*1000:0.0f}")

输出结果:

 predicted price of a house with 1200 sqft, 3 bedrooms, 1 floor, 40 years old = $281683